Difficulty - Medium - Brain Easer

Chess, Difficulty - Medium

Mate in 2 Chess Puzzle 4

White to play and mate in 2

Difficulty - Medium, Geometry

Area of the Rectangle

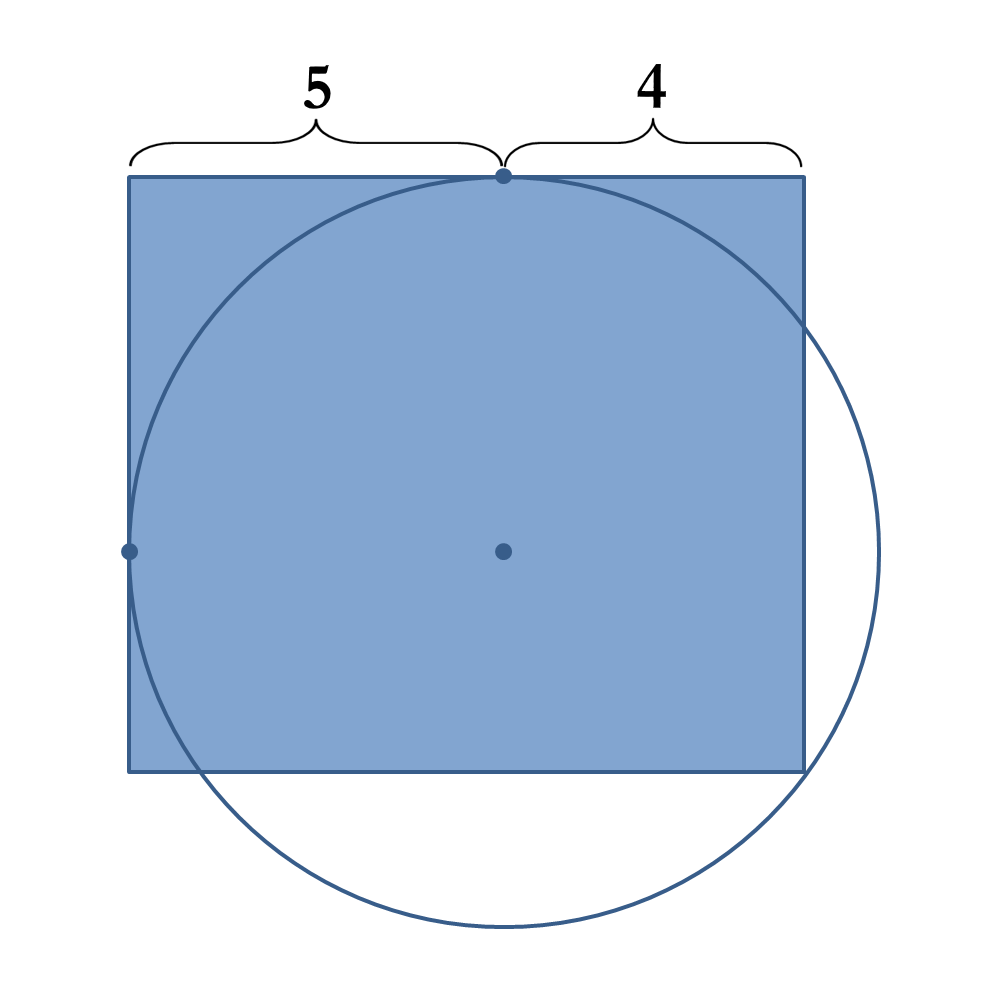
The shaded rectangle is tangent to the circle at the two points indicated, and its bottom right corner lies on the circumference of that circle. What is the area of the rectangle?

Difficulty - Medium, Paradox, Probability

The Monty Hall Problem Explained

The Monty Hall Problem

You are on a game show in which there are three identical doors, one with a car behind it and two with goats behind them. You must pick one door, and you win if that door has the car behind it.

After you pick a door, the host of the game show always opens a door you didn’t choose that has a goat behind it. This leaves the door you chose and one other remaining door, and you are given the option to switch your choice to the other remaining door.

Should you switch or should you stick to your original choice? What chance of winning would that give you?

The History

The Monty Hall Problem is a classic probability puzzle, named for its similarity to the game show “Let’s Make a Deal”, which was hosted by Monty Hall. The problem was made famous when Marilyn vos Savant answered it correctly in her column in a popular magazine, and thousands of readers wrote letters to the magazine arguing her solution was wrong!

The solution can be counter-intuitive, so give it some thought and then scroll down to see the Monty Hall Problem explained.

Difficulty - Medium, Matchstick Puzzles, Simple Math

7 Matchstick Equation Puzzles

In matchstick puzzles, you are presented with an incorrect equation made using matchsticks, and you must move 1 or more matchsticks to turn it into a valid equation.

You must use all of the matches, and you are not allowed to make an inequality symbol such as ≠, ≥, >, <, or ≤.

In each of these 7 fun matchstick equation puzzles, move exactly 1 match to fix the equation:

Click for Solution to 1 + 2 = 8

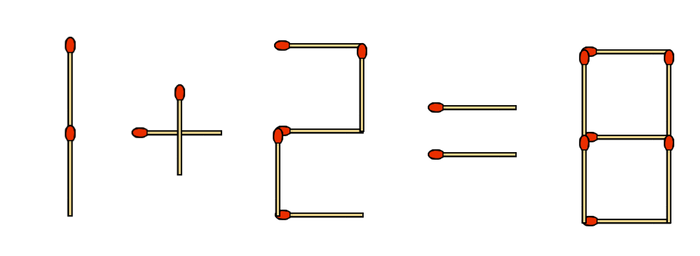
7 + 2 = 9

Difficulty - Medium, Interview Brain Teasers, Logic Puzzles

Color of the Last Ball

There is a bag with 20 blue balls and 13 red balls. Randomly remove 2 balls from the bag:

If they are the same color, replace them with a blue ball
If they are different colors, replace them with a red ball

Repeat this process until there is just 1 ball remaining. What is the color of the last ball?

View Solution

Difficulty - Medium, Number Theory

Multiple of 24

Prove that for all prime numbers p > 3, (p² – 1) is a multiple of 24.

Difficulty - Medium, Interview Brain Teasers, Probability

Same Birthday in Line

There is a long line of people waiting to see a new movie. They announce that the first person to have the same birthday as someone standing before them in the line gets to meet one of the actors in the movie.

What place in line would maximize your chances of winning? Assume birthdays are uniformly distributed through the year.

Difficulty - Medium, Number Theory

Digital Sum of the Sum

The digital sum of a number is just the sum of the individual digits. E.g., the digital sum of 123 is 1 + 2 + 3 = 6.

The digital sum of x is 42
The digital sum of y is 67
When x and y are added, you have to “carry the 1” exactly five times (e.g., if you add 8 and 9, you “carry the 1” once to get a “1” in the tens digit, thereby getting 17)

What is the digital sum of z = x + y?