Nob’s Number Tree
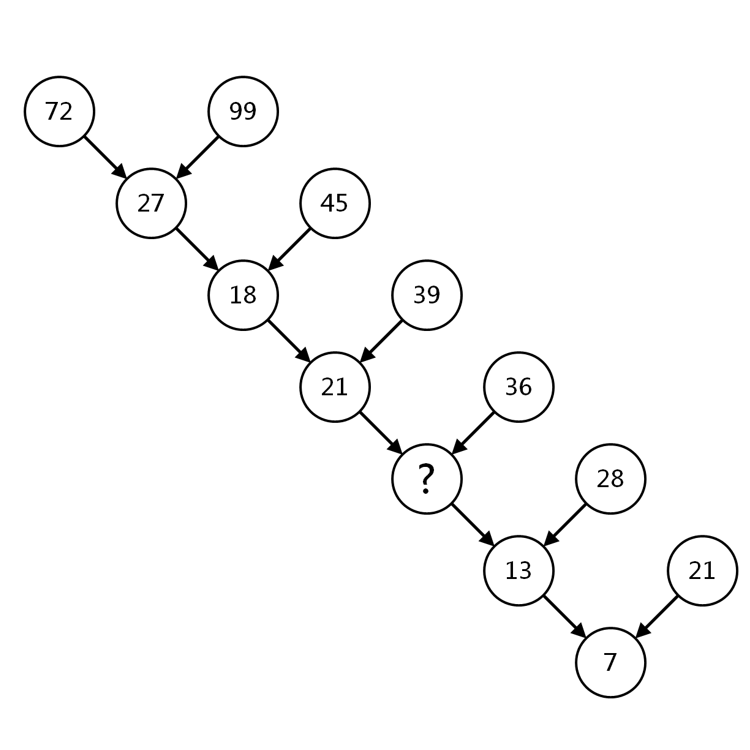
What number belongs in the “?” circle? Note that all numbers shown are correct, there are no typos or errors.
Nob Yoshigahara’s Puzzles
Nob’s Number Tree is a well-known brainteaser by the Japanese puzzle guru Nobuyuki “Nob” Yoshigahara, who wrote many mathematical puzzle books and invented many puzzle toys. This cheeky number tree puzzle seems straightforward, but the straightforward solution falls apart when you arrive at the bottom.
Click to see solution
The answer is 12.
You get this by adding up all the digits in a row to get the number in the circle below. For example, 7 + 2 + 9 + 9 = 27 for the first row. So 2 + 1 + 3 + 6 = 12.
If you thought the solution was 15, you may have fell for Nob’s cleverly-laid trap! 15 unfortunately is not a valid solution.
See, it appears that you can just take the difference between the two numbers in a row to arrive at the number in the circle below (for example, 99 – 72 = 27). However, this pattern works for most of the rows but does not work for the last row (21 – 13 ≠ 7), and you were told that there were no typos or errors.
However, 2 + 1 + 1 + 3 = 7, which confirms adding the digits is correct, and taking the difference is incorrect.
The puzzle is devious in that Nob selected numbers such that they lead you down the path of an obvious solution – only to dispel the illusion at the end. Many are convinced the last number is an error, until the solution is shown to be simple and straightforward as well.
Liked this Nob Yoshigahara puzzle?
He also designed physical puzzles!
Disclosure: The post contains affiliate links, through which I may earn a small fee if you make a purchase, at no additional cost to you. As an Amazon Associate I earn from qualifying purchases.
Let me know the answer
I tried my best
Sure, you can click or tap on the “Solution” on this page to see the explanation of the answer.
For convenience, the answer is (**spoiler warning**) 12, by adding up all of the digits in the row above it.
Couldn’t understand the solution
Thank you for your feedback. We have re-written the solution to clarify, hopefully that makes it easier to understand.
Damn Braineaser who divulged the solution. What malice. What a lack of consideration. What a jerk..
I see 15. 15 + 21 = 36. 15 +13 = 38. 12 does not fil.
Thank You
So much
Let me learn it
15 works too! Don’t think 12 is the only solution
Nob’s puzzle is clever in that it tries to trick you into thinking 15 is a solution, but unfortunately it actually doesn’t work!
I have expanded the explanation to make it clearer why 15 does not work.
15 also works for a different reason
Number 15 also works. for example, 99-72 = 27. 45-27=18. Also 36-21 = 15. Then 28-15=13.
That’s part of the fun of this puzzle. Unfortunately, the last line shows this method doesn’t work, because 21-13≠7. Click on the solution above to see the full explanation.
Hmmm….I think 15 would work too
It should be 15
Simply if you add the two numbers in each circle the arrow points to the sum of both circles, so I would consider both circles as parentheses that are added to itself internally and then added to by both sums.