In this maze, you must alternate going through blue and red doors – in other words, you cannot go through two blue doors in a row or two red doors in a row.
Entering through the blue door in the top left, can you find your way through the maze and exit through the red door in the top right?

Solution
Yes! The most direct route is shown in magenta below:
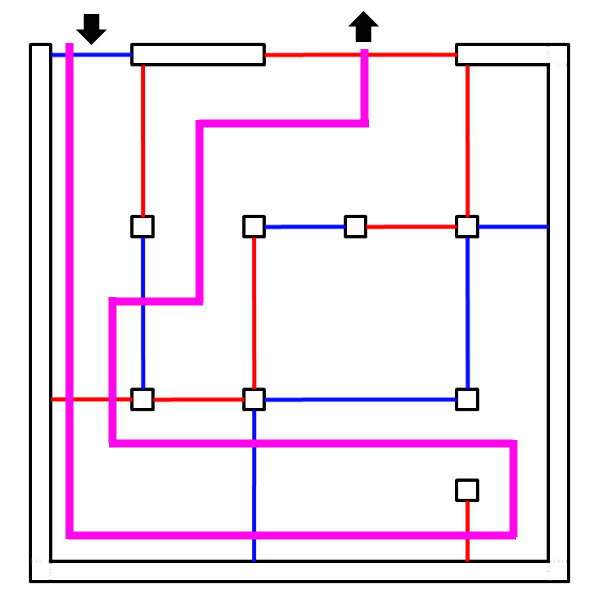
Here is one way of figuring out the solution without using trial-and-error:
- The exit is red, so to successfully exit, you need to enter the room containing the exit using a blue door.
- There are two blue doors to the exit room, but we can rule out the one on the right. In order to pass through the blue door on the right, we must have entered that room using a red door, all of which come from the exit room—but if you were in the exit room and could go through a red door, you would just exit.
- So now we know the solution must pass through the left blue door from the room with the entrance.
- The entrance room has two red doors, but it has to be the one at the bottom because the one at the top leads to the exit room (again, if you’re in the exit room and could go through a red door, you would just exit).
- From there, we’re pretty much done, because there’s only one door of the correct color in each room after that.

I was able to think up a method for analyzing this puzzle, and then I used the method to solve it. (I don’t tell my whole method here, because I don’t want to make a “spoiler”, giving away too much, which might spoil the puzzle for others.) My method involved trying out some paths that did not work, before finding a path that did work. So my method was not totally straightforward, because I did not find the right path on the first try. Now, what are we supposed to learn from this puzzle? Is there something special about this puzzle? How many different methods are there, for solving it? What generalization might I make, upon solving this puzzle? Is this puzzle applicable to some class of real-life practical situations, and if so, what class is that? In real life, if I’m in an enclosure, what practical difference does it make how I got there? The justification for such a puzzle on practical grounds seems convoluted. I can see how there _could_ be such a real-life situation (where one has to gain a key or some information, by going into a different enclosure, before going into “this” enclosure? Do you have any real-life practical example of it, and if so, how many enclosures and door-types are involved in it? How about this for an example: One has to go to college (enclosure A) to get a degree, before getting a job in a certain company (enclosure B). This example is so simple that it doesn’t require such skill as in the above puzzle.
Thanks for sharing your thoughts. The provided solution is the only solution (setting aside solutions that simply add pointless loops to this one). I’ve now added an explanation to show how to deduce the answer without relying on trial-and-error.
You’re right, the puzzle doesn’t really have real-life applications. Here are some fun contrived scenarios I thought of:
– a Kafkaesque bureaucracy in which forms have other forms as prerequisites before you can submit them
– a science fiction maze in which passing through an electrically-charged barrier results in your spacesuit becoming electrically charged, and you can only safely pass through barriers with the opposite charge
Left at first blue. Straight across the next red. Left again at blue. Straight through final red door. Much shorter than official answer.
Left at the first blue is not a valid move, since you entered the maze using a blue door.